Как определить функцию по графику в excel
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.

Как построить график в Excel — Подробная инструкция 2019
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
Построение гистограммы с двумя рядами данных
Перед тем, как приступать к редактированию гистограммы, следует ввести исходные данные. Их лучше расположить столбцами.
После того, как с заполнением столбцов будет покончено, понадобиться сделать следующее:
-
Кликните правой кнопкой мыши по области построения диаграммы. В открывшемся контекстном меню выберите пункт «Выбрать данные».
В поле «Имя ряда» вводим название первого массива данных, а в поле «Значения» выбираем первый столбец на рабочем листе, нажимаем «ОК»
В поле «Имя ряда» вводим название второго массива данных, во второе поле выбираем второй столбец на рабочем листе, нажимаем «ОК»
На этом построение гистограммы закончено. В таком виде ее можно добавить в презентацию PowerPoint, на веб-ресурс, в текстовый документ и т. д.

Как построить график и диаграмму в Excel — подробная инструкция
Математическим исследованием формы цветов и листьев занимался также Хабеннихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т. д. Вот некоторые из этих кривых:
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:



Построение и исследование графиков функций при помощи электронных Таблиц Excel. » | Образовательная социальная сеть
- С чего начинается ввод формулы в ячейку? (Со знака равенства)
- На каком языке набирается формула в MS Excel? (Английском)
- Как скопировать формулу в другие ячейки?(С помощью маркера автозаполнения)
- Как изменить число десятичных знаков после запятой в отображаемом числе? (Выделить, Формат, Ячейки, вкладка Число, Числовой формат, …..)
- Что означает запись ###### в ячейке? (Длина водимых данных превышает ширину ячейки)
- Каким образом набирается формула, содержащая какую-либо функцию? (Выделить ячейку, в которую нужно вставить первое значение функции;Вставка, Функция, выбрать Категорию и саму функцию)
- Каким образом набирается формула, содержащая сложную функцию, например, y = |x 2 |? (Вставляется внешняя функция с пустым аргументом, затем левее строки редактирования формул из раскрывающегося списка выбирается внутренняя функция)
- Как вставить какой-либо символ, например, математический в ячейку? (Вставка, Символ, в появившемся диалоговом окне выбрать шрифт Symbol и нужный символ)
Самый простой график в Экселе — это зависимость одного ряда значений от другого. Рисовать её предельно просто: достаточно задать параметры и сделать несколько кликов мышью. Вполне естественно, на графике будет отображаться только одна линия; если их больше, необходимо вернуться к началу инструкции и проверить правильность совершённых действий.
Скачать:
ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»
учитель математики МБОУ «Многопрофильная гимназия г. Лагани»
1.3. Инструкция по построению кривых в полярных координатах с помощью программы Microsoft Excel
1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента
Актуальность работы. При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые в школьных учебниках по информатике не оговариваются.
Вопрос (мотивация ): Как построить график с изменяющимся параметром, для дальнейшего его изучения?
Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и уравнений степеней выше второй с двумя переменными.
Гипотеза: для решения поставленной проблемы, возможно использовать инструменты прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.
Поэтому, объект нашего исследования — прикладная программа Microsoft Excel, ее возможности для построений графиков функций и исследования их .
Исходя из этого, предметом нашего исследования стали уравнения элементарных функций и кривых высших порядков.
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:
- Научился строить графики функций, с дальнейшей возможностью изучения их свойств
- изучил переход от декартовой системы координат к полярной и обратно;
- исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
- познакомились с некоторыми замечательными кривыми известных математиков.
Планы и перспективы: продолжить изучение плоских кривых.
Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.
Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.
Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение функции.
Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования
. Рассмотрим в качестве примера тригонометрическую функцию
Для дальнейших исследований будем одновременно строить график исходной элементарной функции y= sinx и преобразованной функции и сравнивать полученные результаты.
Формулы будут записаны в терминах электронных таблиц следующим образом:
А3= -7
А4 =А3+0,1 (шаг можно уменьшить например до 0,001)
B3 =sin(a3)
у меня независимая переменна изменяется на интервале (-7;7), что примерно соответствует интервалу ( )
В ячейке F1 будем задавать значение параметра k, и рассматривать полученные изменения графика функции
Фрагмент произведенных расчетов из электронной таблицы приведен ниже
В приложенном к работе файле Microsoft Excel работа графики можно увидеть полные вычисления и полученные результаты
Для детального изучения преобразований графики построил в одной системе координат, что дает возможность сравнить полученные результаты.
Для дальнейших исследований достаточно теперь изменить значение в ячейке f1, и получим иную картину. Например f1=-4
Как видно значения функции автоматически пересчитаны, и построен уже другой график. Данные возможности мною были продемонстрированы одноклассникам на уроке математики. В дальнейшем мои товарищи на уроки изучили свойства полученных графиков функций и наглядно изучили преобразования графиков следующих функций
Мои исследования, на этом не закончились, возник вопрос в построении более сложных графиков. В качестве примера мною рассмотрено уравнение
В полярной системе координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел . Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).
Связь между полярной и декартовой системами координат.
Точка О — полярный полюс , луч ОЕ будем называть полярной осью , отрезок ОМ — называют длиной полярного радиуса R , п оложительный угол от луча ОЕ до луча F — полярный угол .
Если известны полярные координаты R и , точки М , то можно уставить связь с её декартовыми координатами.
Построим прямоугольный ОМЕ . В этом треугольнике гипотенуза ОМ = R , ЕОМ = , катет ЕМ = у , катет ОЕ = х координаты точки М .
Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: , , . Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: , затем , .
Некоторые замечательные кривые. На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея, Фибоначчи, кардиоида, овалы Кассини, лемниската Бернулли, фигуры Лиссажу, розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези) и т.д.
в полярных координатахс помощью программы Microsoft Excel.
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.
Решение. Найдем уравнение данной линии в полярных координатах.
Предположим, что угол F изменяется в интервалах от 0 до 2 . Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.
Формулы будут записаны в терминах электронных таблиц следующим образом:
А2 0,1 А3 =А2+0,1 B2 =4*COS(3*F)
C2 =SIN(А2) D2 =COS(А2) E2 =B2*D2 F2 =В2*C2
Тогда получаем следующее распределение по столбцам электронной таблицы:
Для построения графика выделим информационный блок E2..F64, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д. Получим следующий график.
Исследование формы кривой , в зависимости от изменения значений входящих в её уравнение. Внося изменения в ячейку H27 , не меняя более ничего, мы можем получать различные виды уравнения
Обратимся к исследованию формы роз. Поскольку правая часть уравнения не может превышать величины a , то и вся роза, очевидно, уменьшается внутри круга радиусом a . Количество же лепестков розы зависит от величины модуля k :
1. Если модуль k – целое число, то роза состоит из k лепестков, при нечетном k , и из 2 k лепестков при k четном.
2.Если модуль k – рациональное число, равное то роза состоит из m лепестков в случае, когда оба числа m и n нечетные, и из 2 m лепестков, если одно из этих чисел является четным.
При этом, в отличие от первого случая каждый следующий лепесток будет частично перекрывать предыдущий.
3.Если модуль k – иррациональное число, то роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга.
Математическим исследованием формы цветов и листьев занимался также Хабеннихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т. д. Вот некоторые из этих кривых:
В полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений:
1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента
Свои исследования я продолжил, возник вопрос в построении графиков функций состоящих из нескольких кривых на заданном интервале. В качестве примера мною рассмотрено построение эскиза калмыцкого орнамента (геометрического) в Excel.
Если рассмотреть любой геометрический орнамент, то с математической точки он представляет собой набор прямых или кривых на заданном интервале, иногда на одном интервале может быть задано несколько различных линий. Совокупность этих линий и кривых образует рисунок который и будем считать орнаментом.
Также можно заметить, что орнамент представляет собой периодическую функцию (рисунок повторяется, через заданный интервал). Для того, чтобы построить заданный орнамент мы его построим на определенном интервале, а затем перенесем все вычисления на заданный шаг и т. д.
Приведенный ниже орнамент представляет собой семейство прямых заданных на отрезках, причем прямые параллельны одной из осей координат т.е. их уравнения принимают вид у =a или х =а.
(Полные вычисления можно увидеть в файле приложении1)
Проделав данную исследовательскую работу я пришел к следующим выводам: Microsoft Excel предоставляет большие возможности для построения и исследования графиков функций.
Изучая кривые линии высших порядков, ведь используя Microsoft excel, это не составляет труда, мне представился удивительный мир графиков различных функций. Оказывается таким образом можно построить, меняя параметры в данных уравнениях графики, которые напоминают листья растений и деревьев (например: кувшинки или лотоса). Оказывается математика — живая наука.
Опыт, приобретенный мною в процессе выполнения работы, несомненно, пригодится мне в дальнейшей жизни. Так, например, умея строить графики уравнений с параметрами можно найти корни уравнений и их зависимость от введенного параметра, что даст наглядную картину решения данного уравнения. Это позволяет решать задания ЕГЭ по математике части С5.
Также данные навыки будут необходимы при построении графиков и диаграмм в дальнейшей профессиональной деятельности, так excel прикладная программа применимая во многих сферах деятельности человека, например бухгалтерии, дизайн, аналитика, инженерия и другие.
2) найти возможности программы Excel для решения этой задачи. Как я говорил, в данной программе, много возможностей, многие из них, я еще не изучил.
3) найти другие программы построения графиков, которые позволят построить график данных функций. Такие программы существуют, например Adgrapher или DPlot и др. Данные программы, я планирую изучить в дальнейшем. Оптимальным решением, конечно же, будет создание своей программы, используя языки программирования.

Как построить график косинуса в excel
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Процесс создания графика в приложении Excel 2003, 2007
Порядок построения диаграмм в приложении Эксель 2003 является похожим на процесс работы с программой Эксель 2007.
Результаты вычислений выполняют роль исходных данных в процессе создания диаграмм.
Порядок формирования графика в Экселе 2003 включает в себя следующие этапы:

- В самом начале запустите приложение и откройте новый лист книги. Далее сделайте таблицу из двух столбцов. Первый столбец будет использоваться для записи аргумента (X), а второй – для функции (Y). Как это выглядит, вы можете увидеть на картинке, размещенной ниже.

- На следующем этапе внесите в столбец B аргумент X. Затем в столбец C вносится формула, которая будет применяться для построения графика. В качестве наглядного примера мы возьмем довольно простую формулу y = x 3 . Как это выглядит, вы можете увидеть на расположенной ниже картинке.
Следует помнить, что в данном приложении перед любой формулой нужно ставить знак «=».
В нашем конкретном примере формула, которую необходимо внести в столбец C, будет выглядеть так: =B3^3, т.е. программа будет возводить значение из ячейки B3 в третью степень.
Также вы можете использовать и альтернативную формулу, которая будет выглядеть, так: =B3*B3*B3. После внесения формулы в столбец C следует нажать «Enter» .
Так как внесение формулы в каждую ячейку является долгим и достаточно трудоемким процессом, разработчики Эксель позаботились о комфорте пользователей.
Для того чтобы внести формулу во все ячейки, достаточно просто растянуть заполненную.
Эта особенность является одним из главных преимуществ Эксель, позволяющая упростить работу с приложением. Также напоминаем, что ячейки можно объединять между собой.
Вам необходимо щелкнуть по заполненной ячейке, в которой находится формула. В нижнем правом углу этой ячейки вы сможете увидеть небольшой квадратик.
На этот квадрат нужно навести курсор, зажать правую кнопку и растянуть формулу на все незаполненные ячейки.
Как именно это, делается вы можете увидеть на картинке, размещенной ниже.

- Затем вам необходимо выбрать подходящую из доступных точечных диаграмм и нажать кнопку «Далее» . Следует выбирать именно точечную диаграмму, потому что остальные типы диаграмм не дают возможности задать аргумент и функцию в форме ссылки на заполненную вами группу ячеек. Процесс выбора подходящей точечной диаграммы показан на картинке, размещенной ниже.
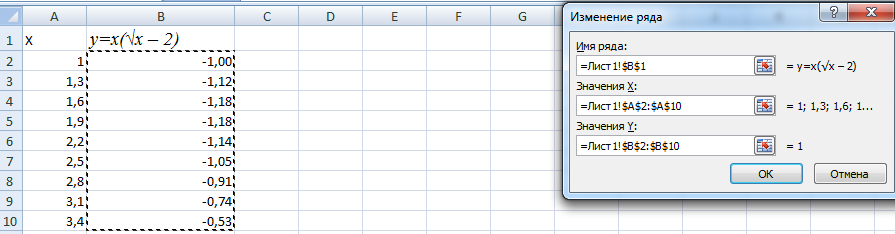
- На следующем этапе перед вами возникнет окно, в котором необходимо открыть вкладку под названием «Ряд» . Затем следует добавить ряд при помощи специальной кнопки под названием «Добавить» . Для выбора ячеек необходимо нажать на кнопки, которые показаны на размещенной ниже картинке.

Вам потребуется выделить ячейки, в которые вы ранее внесли значения Y и X. Затем необходимо нажать кнопку «Готово» .
При необходимости вы можете изменить значения аргумента и функции, что приведет к мгновенному перестроению созданного графика.
Кстати, вас могут заинтересовать еще статьи:

Важно: работа в MS Excel мало отличается от пользования бесплатными редакторами. Посчитать проценты или создать график в любом из них можно, следуя приведённой далее инструкции — нужно лишь слегка адаптировать её под конкретный программный продукт.
Как построить график или диаграмму в Microsoft Excel 2003, 2007, 2010, 2013, строим синусойду и круговую диаграмму, линейная функция, мастер диаграмм
- На следующем этапе необходимо внести в таблицу значение аргумента, а в первую ячейку второго столбца следует внести формулу =SIN(C4). После того как вы внесете формулу в ячейку, необходимо растянуть ее таким же способом, как было описано выше, на все незаполненные ячейки. Процесс заполнения столбца с формулами вы можете увидеть на картинках.
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.





