Дисперсионный анализ: соединение теории и практики

Минимальное число классов градации (групп) — два. Классы градации могут быть качественными либо количественными.

Дисперсионный анализ — почти универсальный метод проверки различий в группах, поскольку применяется как в технических науках и маркетологии, так и в исследованиях поведения человека.

Как формулируются, принимаются и отвергаются гипотезы при дисперсионном анализе? При дисперсионном анализе определяют удельный вес суммарного воздействия одного или нескольких факторов. Существенность влияния фактора определяется путём проверки гипотез:

Ещё некоторые понятия дисперсионного анализа. Статистическим комплексом в дисперсионном анализе называется таблица эмпирических данных. Если во всех классах градаций одинаковое число вариантов, то статистический комплекс называется однородным (гомогенным), если число вариантов разное — разнородным (гетерогенным).

В зависимости от числа оцениваемых факторов различают однофакторный, двухфакторый и многофакторный дисперсионный анализ.

P-value AB-теста как раз и показывает, насколько редкое событие мы наблюдаем, если бы предложение вводить номер телефона на самом деле (на длительном периоде времени) ничего не улучшало, а возможно даже и ухудшало.

На что мы обращаем внимание при расчете статистической значимости A/B-теста / Хабр

Чем более точными требуются расчеты, тем меньший коэффициент α используется. Естественно, что статистические прогнозы в физике, химии, фармацевтике, генетике требуют большей точности, чем в политологии, социологии.

малый	средний	большой
48	47	46
50	61	57
63	63	57
72	47	55
43	32
59	59
58
Среднее	58,6	54,0	51,0
Дисперсия	128,25	65,00	107,60

3.Корреляционно-регрессионный анализ в Excel

На основе данных таблицы построим уравнение регрессии: у_х=2,836-0,067х. Коэффициент регрессии а₁=-0,067 означает, что с повышением урожайности зерновых на 1 ц/га затраты труда на 1 ц зерна уменьшаются на 0,067 чел.-ч.

Коэффициент корреляции r=0,85>0,7, следовательно, связь между изучаемыми признаками в данной совокупности тесная. Коэффициент детерминации r 2 =0,73 показывает, что 73% вариации результативного признака (затрат труда на 1 ц зерна) вызвано действием факторного признака (урожайности зерновых).

В таблице критических точек распределения Фишера — Снедекора найдём критическое значение F-критерия при уровне значимости 0,05 и числе степеней свободы к₁=m-1=2-1=1 и k₂=n-m=30-2=28, оно равно 4,21. Так как рассчитанное значение критерия больше табличного (F=74.9896>4,21), то уравнение регрессии признаётся значимым.

Для оценки значимости коэффициента корреляции рассчитаем t-критерий Стьюдента:

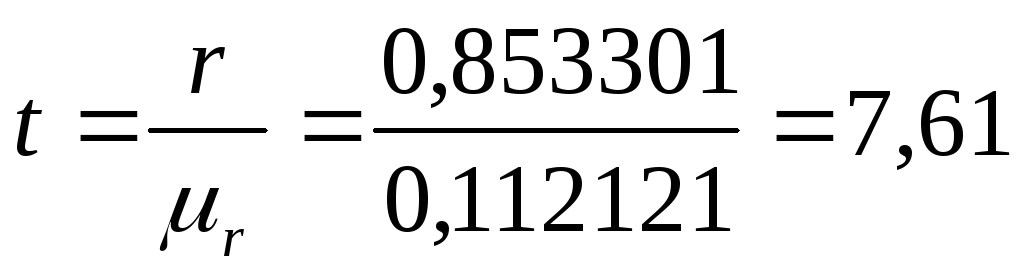
Втаблице критических точек распределения Стьюдента найдём критическое значениеt-критерия при уровне значимости 0,05 и числе степеней свободы n-1=30-1=29, оно равно 2,0452. Так как расчётное значение больше табличного, то коэффициент корреляции является значимым.

На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:

Оценка значимости коэффициентов регрессии

Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.

Методы досрочного завершения теста

Pocock

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.

O’Brien-Fleming

Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента :

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.

Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α . Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α .

Уровень значимости в статистике.

1. Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
2. Определяем срок, на который запускается тест.
3. Случайно разбиваем пользователей на две группы.
4. Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
5. В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
6. По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
7. Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.

Взять исходные данные согласно варианту работы (по номеру студента в журнале). Задан статический объект управления с двумя входами X₁, X₂ и одним выходом Y. На объекте проведен пассивный эксперимент и получена выборка объемом 30 точек, содержащая значения Х₁, Х₂ и Y для каждого эксперимента.